Tracing the link between a geometric tangent and the modern tangent function.
I created this page so I could answer a simple question: why do the tangent function and tangent line share a name? The concepts here are elementary in trigonomery courses, but the "why is it called that" is rarely covered and I was curious.
Mathematics is full of repeated terms whose historical connections are easy to miss. One of the most common is the tangent function and the geometric tangent line. Why would a function that gives the ratio of two sides of a triangle share a name with a line that touches a circle at a single point and why do diagrams such as the two included below label the length of a segment of a line tangent to the unit circle as the tangent function?
The word “tangent” comes from the Latin tangere, meaning “to touch.” A tangent line to a circle touches it at exactly one point. If we consider a unit circle and draw such a tangent line, we can define a trigonometric function directly from this geometric configuration.
The tangent function is often defined algebraically as:
\[ \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \]
But where does this definition come from? Geometrically, we define sine and cosine as the vertical and horizontal coordinates of a point \( A = (\cos(\theta), \sin(\theta)) \) on the unit circle. The line from the origin \( O \) to \( A \) has slope:
\[ m = \frac{\sin(\theta)}{\cos(\theta)} \]
This slope is the key to understanding why the tangent function and tangent line are connected, not because we assume the tangent function is this ratio, but because the geometric construction requires it.
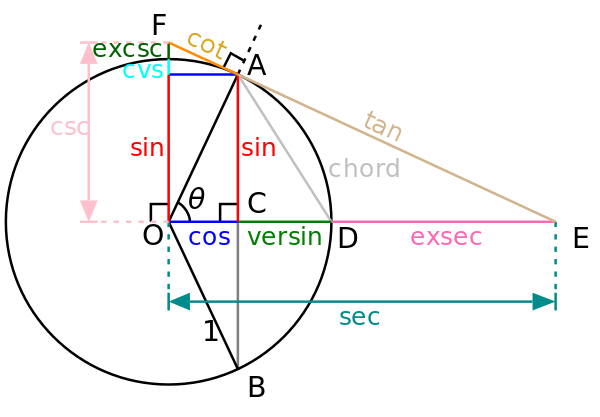
Diagram modified under GNU Free Documentation License.
The goal was, given just the angle between the observer and a point of interest, to find the height of the point above a location some known distance away (we assume one unit of distance for simplicity). We call the function that returns the height given the angle the tangent function.
Slightly more formally:
The equation of the line \( \overrightarrow{OA} \) is:
\[ y = \frac{\sin(\theta)}{\cos(\theta)} x \]
Substitute \( x = 1 \):
\[ y = \frac{\sin(\theta)}{\cos(\theta)} = \tan(\theta) \]
So the segment from the x-axis to point \( E \) has length \( \tan(\theta) \).
A builder measures the angle of elevation to the top of a tower to be \( 21.8^\circ \) from a point 500 feet away. What is the height of the tower?
First, we calculate the sine and cosine: \[ \sin(21.8^\circ) \approx 0.3717, \quad \cos(21.8^\circ) \approx 0.9283 \] Then: \[ \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \approx \frac{0.3717}{0.9283} \approx 0.4 \] Now compute height: \[ h = d \cdot \tan(\theta) = 500 \cdot 0.4 = 200 \text{ ft} \]
So the tower rises approximately 200 feet above the observation point.
The tangent value represents the height along a vertical line at distance \( d \) from the observer, exactly the same as our construction using the vertical tangent line at \( x = 1 \).
Let’s return to the unit circle. If we draw a tangent line to the circle at point \( A \), and let it intersect the x-axis at point \( H \), then the triangle \( \triangle OAH \) is similar to the triangle \( \triangle OED \), where \( E \) is the point where \( \overrightarrow{OA} \) intersects the line \( x = 1 \), and \( D \) is the foot of the perpendicular from \( E \) to the x-axis. In otherwords \( \triangle OAH \) is just \( \triangle OED \) rotated and mirrored, so the length of the \( \overrightarrow{AH} \) side is \(\tan(\theta)\).
Both triangles share angle \( \theta \), have a right angle, and have a side of length 1 from the origin to the point on the circle. Since similarity preserves ratios, and since the vertical side of triangle \( OED \) has length \( \tan(\theta) \), so must the vertical side \( AH \) of triangle \( OAH \).
This triangle-based interpretation confirms the geometric origin of the tangent function: it measures the height where a ray at angle \( \theta \) intersects a vertical line one unit away, or equivalently, the length along the tangent line from the point of contact to the x-axis.
So in the end, the tangent function was named for its geometric construction on two tangent lines: the vertical line used to relate angle to height and the length of the line segment collinear with the tangent line that intersects the unit circle at point A in the diagram. That line is what the animation shows in green and the first diagram has lablelled "tan".